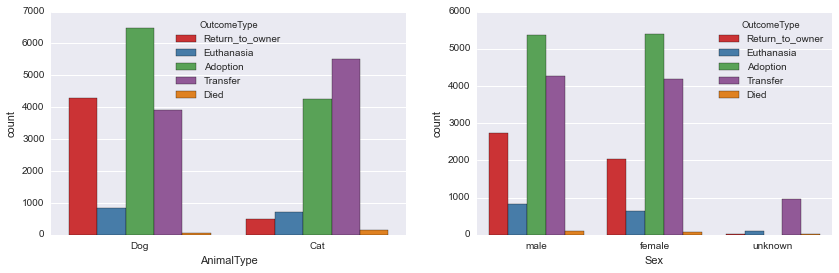
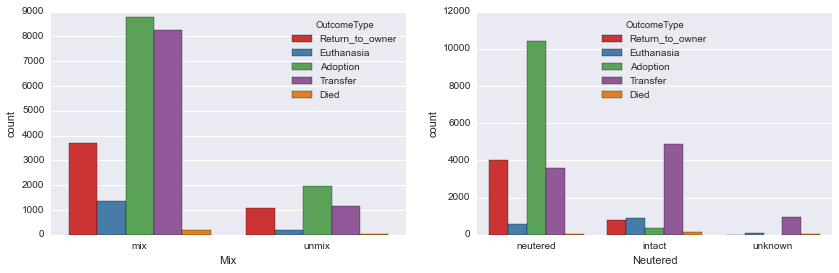
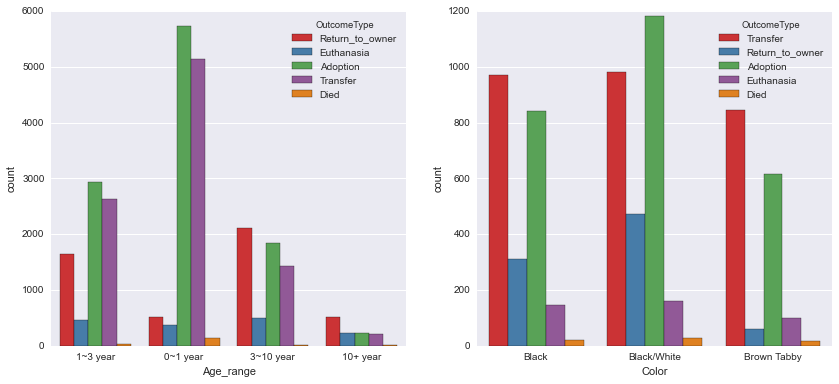
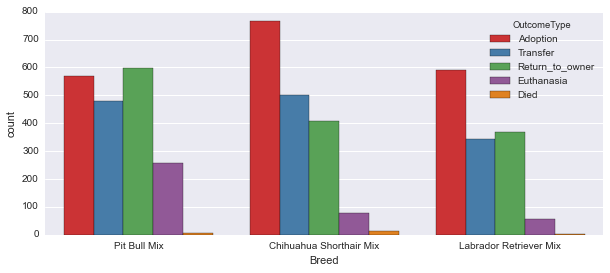
平稳性

平稳性是大多数时间序列分析问题中的一个大前提，而通常我们讨论的都是弱平稳，需要满足以下几个条件：

1）在任意时间点变量的均值函数是一个常数

2）在任意时间点变量的方差函数是一个常数

3）在任意两个时间点的自协方差函数只与两点时间间隔有关，而与这两点具体的时间点无关

典型的平稳时间序列：白噪声 $N(t)$

典型的非平稳时间序列：random walk（$R(t) = \sum_1^t N(i)$，方差随时间改变）

如果时间序列不满足平稳性，可以做N阶差分运算。

自相关

时间序列的自相关性，从字面上就可以看出来，就是看这个序列平移一段距离后与这个原始信号有多相似。

有点类似于卷积，但符号刚好相反。

1
2
3
4
5
6
7

import numpy as np
t = np.linspace(0, 20, 10000)
ts = np.sin(2*np.pi*0.2*t)
ts = ts - ts.mean()
autocorr = np.correlate(ts, ts, mode = 'full')
autocorr = autocorr[ts.size:] / autocorr.max() #归一化
plt.plot(autocorr)

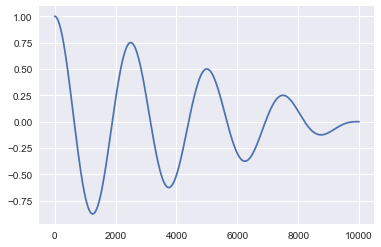
一般来说，平稳时间序列的自相关函数会随时间快速衰减。

其实本来是想看看关于时间序列分析的资料来应用到KDD CUP 2017的比赛上，而且之前天池上O2O口碑商家销量预测也是一个类似的时间序列问题。但是反复琢磨了一下，题目最终的预测只是在rush hours中的一两组数据，真正关于时序的信息可能真的用不大，而且之前口碑比赛里也有相应的反应，像ARIMA这种模型效果并不理想，所以下一步可能会考虑模式匹配的方法来做。

Word2vec，顾名思义，就是把词语料中的所有词转化为向量形式，这样自然语言就有了数学表达形式，向量化后可以聚类、近义词等运算，举一个论文中的例子，vec(“Madrid”) - vec(“Spain”) + vec(“France”)所生成的向量与vec(“Paris”)的距离是最近的。同样对于机器学习模型来说，也可以将词作为embedding的特征输入。另外，由于作者Tomas Mikolov在深度学习领域下比较出名，所以word2vec也自然而然的被归到“深度”网络了，然而了解原理后就会发现其实就是一个2-layer的浅层模型。

主要建模的方法有CBOW和Skip-gram两种，每种方法下面又可以分为Hierarchical Softmax和Negative Sampling方法。虽然看上去有点复杂，但是大致的原理很相似，下面就尽量以简单的语言和逻辑给出word2vec的原理。

CBOW

首先来看一下CBOW（Continuous Bag of Words）模型的基本结构。假设要预测词$w(t)$的向量，那么输入层是与$w(t)$相邻的几个上下文词，投影层是对这些上下文进行了向量求和运算，而输出层就是$w(t)$的概率表示。整体上来看，假设临近的词都具有一定的相似性，那么对于CBOW模型而言，目的就是要在给定词$w$上下文$Context(w)$的条件下使$w$的概率最大，这里就可以用到最大似然的思想，目标函数可以定义为对数似然函数，即

显然，对于输入层已经有了明确的表示，可以看做是监督训练中的feature，而现在的问题就是如何去构造输出层的形式，使这个两层网络能够拥有(feature, label)的形式进行迭代训练。这里就要引入另一个概念——霍夫曼编码，目的是对语料中的所有词基于出现的频率进行不等长编码。

简单举个例子就可以很轻松的理解霍夫曼编码的概念。假设我们的语料为{a, b, c, d, e}，这些词在语料中出现的频率为{4, 5, 6, 8, 10}，现在我们就可以基于语料来建立一棵霍夫曼树，如下图。构建过程也很简单，即将目前集合中所有元素的两个最小值进行合并，然后用这两个最小值的求和项来代替两个最小值产生新的集合，重复这一过程直至集合中没有元素，构建过程也在下图中清晰的画了出来（这里人为规定左子节点的值大于右子节点的值）。这样看来，语料中的所有词语都会是一个单独的叶子节点（个数为size(语料)），而中间的非叶子节点就是每次的求和项（个数为size(语料)-1）。如果定义霍夫曼树中的左子节点编码为1，右子节点编码为0的话，那么每个词语都可以被唯一且不等长的编码。例如a可以被编码为100，d可以被编码为01。可以看到频率越高的词语就越出于根节点的位置，编码长度也就越短，在通信里传输数据量也就越小，这也是通信里不等长编码的奥妙所在（把本科的东西再捡起来）。

Hierarchical Softmax

OK，现在我们已经有了每个词语的霍夫曼编码，该考虑如何构建$p(w|Context(w))$了。以词语d为例，观察之前构建的霍夫曼树结构可以发现这个词语进行了两次叶子分叉：第一次从根节点分到了右子节点，第二次从当前根节点分到了左子节点。这里Hierarchical Softmax的思想就体现了出来，即把每一次非叶子节点的分裂都视为是一次二分类问题，对应的类别就是0/1，也就是节点上的编码值。如果定义1为负类，0为正类（反过来也可以），并在每次分类时采用逻辑回归模型，那么词语d的两次分类概率分别为

其中$\sigma$为逻辑回归函数$\frac{1}{1+e^{-y}}，$ $v(d)$是词语d上下文的向量求和，$\theta$为每个非叶子节点所对应的辅助向量，维度与词语的向量维度一致。这样一来，把上面两个概率公式相乘后就可以以霍夫曼编码的形式得到$p(w|Context(w))$了，而每个词语的条件概率通式就可以写出来了，即

这里的$j$是每个词$w$所经过的霍夫曼树路径，$d\in {0,1}$，为在路径上的每一次分类结果。我们的目标就是取上式的似然函数$L(w,j)$最大值，未知参数只有$x_w$和$\theta_w^{j-1}$（每个词对应霍夫曼树路径上的每一个非叶子节点辅助向量），使用随机梯度上升法，不具体推导，直接给出参数的梯度：

这里的参数$\theta$可以直接利用梯度进行更新，但前面我们提到过，$x_w$实际上是$w$上下文的向量求和，而我们真正需要的是$w$的向量$v(w)$，所以在更新$v(w)$的时候需要将梯度贡献到这个词所包含的所有上下文中，并最终生成语料中每个词的词向量，学习结束。

Negative Sampling

看完Hierarchical Softmax方法后，最直观的印象可能就是霍夫曼树的构造过于麻烦，而且当语料库规模很大时，树的复杂度也随之提高，从而导致一定的训练效率问题。Negative Sampling则不采用霍夫曼树进行概率的层次计算，而是采用一种更直观、更简洁的方法。

事实上Negative Sampling可以分为两部分，一部分为Negative，另一部分为Sampling，我们先从Negative说起。如果给定词$w$及其上下文$Context(w)$，我们将此$w$视为一个正样本，其余的所有词都可以看做是负样本，除此之外再直接为每个词分配一个类似于Hierarchical Softmax方法中的辅助向量$\theta$。借助逻辑回归的思想，对于一个词$u$在$Context(w)$条件下分类后的概率为

其中$L_w(u) \in {0,1}$，表示$u$是否等于$w$（需要注意的是由于我们现在讨论的还是CBOW的方法，因此这里的$x_w$和Hierarchical Softmax中的定义一样，依然是$context(w)$的向量求和）。显然，正样本只有一个，而负样本量过大，因此需要采样处理，用$Neg$表示语料中对于$w$采样后的负样本，我们的目标就是最大化

换句话说，就是使正样本概率尽可能高，负样本概率尽可能低。上面的式子只是针对一个词，如果是对于整个语料库$A$，依然是最大似然的思想

待更新参数依然为$x_w$和$\theta_w$，更新依然是梯度上升法，与Hierarchical Softmax基本一致，只不过后者在$\theta$的更新是基于霍夫曼树非叶子节点路径的更新，而前者则是基于$w$的正负样本做更新。

说完了Negative，还有一个重要的Sampling。从上面的基本原理中我们可以看到，负样本相对于正样本要多很多，因此需要对负样本做一定程度的采样，而采样的原则需要保证语料中词频大的词采样概率大，词频小的词采样概率小，以符合原始分布。这样看来就是一个带权采样的问题，具体解决方法可以定义每个词为其词频长度的线段，然后将所有词线段首尾相接连在一起，词频大的词自然线段就长。在采样时随机选取（0，线段总长度）的数字，采样就选择它落在范围内的词，这样就保证了采样后的词与语料中原始词的词频基本同分布。

Skip-gram

Skip-gram与CBOW的唯一区别就在于：CBOW是对$p(w|Context(w))$进行建模，而Skip-gram则是对$p(Context(w)|w)$进行建模。上面一张图可以很好的诠释二者的区别。这里的投影层只是为了和CBOW形势保持一致才加上去的，实际上不起任何作用。

针对Hierarchical Softmax方法，只需要将条件概率形式稍加改变即可

接下来流程完全一致，最大似然，梯度更新，迭代学习。

而对于Negative Sampling也是同样，当给定$w$时，最大化$context(w)$中所有词的似然函数，只需要将优化目标变为

接下来也都是老套路。

结语

关于方法的优劣和数据集、超参数以及语义评价标准有着密切的关系，因此在实际应用中也需要不断的尝试。word2vec的应用也有很多，比如将一个用户的购物历史、app浏览历史等作为一个句子，便可以学习出商品、品类或app的语义特征。google的单机多线程的code执行效率也很高。最近的一个工作是将用户的浏览的品类历史作为句子，学习出每个品类的vec，然后喂给后续的模型作为特征进行训练，只可惜特征重要性并不出众。

引言

两天前南大周志华教授在arXiv上放了一篇文章：Deep Forest: Towards An Alternative to Deep Neural Networks。国内机器学习界瞬间爆炸，业内著名非著名人士纷纷前来解读，有说即将取代DNN的，有说其实没什么新玩意就是那么回事的。我们这里只阐述这个model的基本结构和原理，不做任何评价（个人认为在相同资历和学术水平上才真正有资格去评价，反正我是没资格）。

Architecture

首先，Deep Forest，换一种叫法，gcForest(multi-Grained Cascade forest)，可以翻译为多粒度级联随机森林。通俗的来讲就是把若干个随机森林合并起来作为类似于神经网络中的一个layer，然后将这些layer串联起来，形成一个基于组合随机森林的、相对deep的模型。通过这个描述，模型的主体结构就已经基本形成了，如下图

这里level就是layer的概念，而我们发现Forest有黑色和蓝色两种，其中黑色代表传统意义上的随机森林，即每次选择sqrt(#Features)数量的特征作为候选特征进行分裂；蓝色代表“完全随机森林”，其中每个森林中包含1000棵树，每棵树随机选择特征进行节点的分裂使树一直生长到叶节点只包含同类样本或小于是个样本。因为随机森林本质上就一种ensemble method，而每一个layer又引入了若干个两种随机形式的随机森林，因此在layer层面上可以认为是“ensemble of ensemble”。
现在具体到一个layer，如下图，假设现在是个三分类问题，那么每个随机森林的输出都是这三个类别的概率值，因此对于任何一个样本而言，在每一个layer的每一个forest输的都是3维的向量，如果每一个layer有4个forest，那么在这个layer上就输出43维的新特征灌到下一个layer里。注意，如果不是最后一层，那么每一层接收的特征还要加上raw feature，也就是第N+1层比第N层多出了43个特征。如果是最后一层，就不再接收原始特征，把上一层的输出结果做平均再取最大值，作为最后的prediction。还有一点很重要，也是区别于DNN的最显著因素，就是gcForest每一层都是监督学习，都利用到了label的信息，而非像DNN一样只在最有一层才是有监督而进行误差传播。这样的好处就是可以每向后训练一层就用validation set评估一下accuracy和loss，因为每一层的输出结果都是可解释的，都可以拿来当做预测得分，因此如果训练N+1层时验证效果提高不大或有降低时，可以自适应的终止训练。在这点上DNN必须在训练前就指定layer的层数，相当于变相多了一个超参数。

Multi-Grained Scanning

这算是论文的另一个亮点吧，主要描述了如何由原始数据生成样本和特征，依然还是先看下图。对于序列数据，假设特征是400维，现在我们用一个100维的滑动窗口（实际上窗口也是可变的，并不是只有一个窗）来做window-slide（比较类似于1D-convolution），每滑动一次生成100维向量就作为一个新的样本，这里相当于把原始数据做了滑动拆分，最终形成301个100维特征的子样本。接下来把这些样本灌到Deep Forest的第一层，一个Random Forest为301个子样本生成3个新特征，一个Complete Random Forest也为301个子样本生成3个新特征，然后再将这些特征做一个concat，这样一来一个真正的400维特的样本在第一层输出的高阶特征就是23301维。后面的训练过程就和上面写的一样，一层接一层，直到模型精度改善不明显的时候就终止。而对于图像数据也同理，只不过window-slide由一维变为二维（类似于2D-convolution），不再赘述。整体流程如下图，画的非常明白。

DF vs DNN

再来看DF与对标对象DNN的参数对比，也是文章比较骄傲的一点。在训练DNN时候我们需要指定一大堆超参数，最常见的比如layer数、neuron数、dropout rate、batch size等等。但DF完全不用考虑这些超参，只用默认的参数就很好了。

Performance

不多说，直接上图。

总的来说，这些评估结果都是基于小数据集的，在大数据集上还没测试过。但不可否认的是，相对于DL来讲效率还是要快不少，而且也没用到GPU资源。要知道现在普遍大公司里计算资源已经不是瓶颈了，而是如何把这些复杂的算法在线或是移动端应用起来，所以在这种趋势下，文章提出的这种方法还是极有意义的。

引言

矩阵分解可以视为无监督学习的一种形式，成名于Netflix Prize推荐比赛，由Yehuda Koren引申出诸多变种，在推荐系统中可谓是简单粗暴，非常有效。

矩阵分解，顾名思义，就是把已有的目标矩阵分解为两个矩阵相乘的形式，那么目标矩阵是什么？在推荐系统里一般我们可以理解为是用户（user）-商品（item）-评分（rating）所构成的矩阵。矩阵的每一行代表一个user，每一列代表item，矩阵元素$r_{ij}$代表第i个user为第j个item打得分数，可以是浏览数、加购数、购买数、评论数等等，如果第i个user对第j个item没有任何行为，我们令该矩阵元素为空。而我们的目标就是将这些空元素补齐，用以推断每个user对没有行为的这些item的兴趣度大小究竟是多少，从而找到用户可能最感兴趣的top-K个商品进行推荐。

目标函数

假设矩阵$R$维度为$M \times N$，也就是用户为$M$个，item为$N$个，目标是将$R$分解为$X \cdot Y$的形式，其中$X$维度为$M \times K$，$Y$维度为$K \times N$，$K << M,N$，这里的$K$称为隐因子维度。我们可以把user的隐因子解释为用户的兴趣维度，把item的隐因子解释为商品的属性维度，分解出的结果同样也可以基于cosine similarity计算用户之间的相似度和商品之间的相似度。其实传统的SVD同样也是这种思想，但是由于这里我们的场景有大量的缺失值SVD无法操作，盲目的填补缺失值也会造成模型的过拟合，因此也衍生出了大量诸如SVD++，RSVD等SVD加强版。事实上最基础和原始的矩阵分解优化目标形式非常简洁，思想就是尽可能的可以复原出已有矩阵中非空元素，使预测元素与原始元素保持一致，即

当然，还少不了regulation term，以防止overfitting，这样目标就变得复杂一点

Bias

有了这个基础版本的目标函数，其实就可以在上面进行修修改改，逐步完善。考虑到在实际推荐系统中user和item的多样性，我们还可以在此基础上加上user、item的bias项。举个直观例子来解释这个概念，假如现在要预测用户A对商品a的打分，已经知道的是在所有的商品里均值得分为4分，而a相比所有商品来说质量和口碑要相对好一些，因此均值要高出1分，但用户A又是一个比较较真和挑剔的用户，所以他对每个商品的打分要比所有人打分均值低0.5分，因此如果暂且不考虑兴趣因素，最终A对a的打分可以粗略估计为4+1-0.5=4.5，这里这些均值偏移数据就是所谓的bias项修正。如此目标就又复杂一些

Implicit Feedback

上面说了一大堆，但是有比较核心的一点被忽略了，那就是在现实的应用场景中，“rating”，也就是打分这个概念我们几乎是获取不到的。这相当于是用户给出最积极的反馈，比如豆瓣电影的主动打分，但是大多数用户在网站网行的行为也不过是点击、浏览，在电商场景中可能更多一些，比如关注、加购等，在一些音乐、影视平台上可能有收听、观看和评论等。但总的说来，这些都不能够让我们具体的概化为一个“打分”，或者称为显示反馈，所以需要引入隐式反馈这个概念来进一步刻画矩阵分解的优化目标。

首先引入一个二值变量，定义

这里的$r_{ui}$就不再是打分数据了，而是用户对商品有过任意行为的次数，而二值变量可以理解为一个用户对一个商品有过是/否有过任何行为。接下来优化目标也随之改变

，其中$c_{ui}$称为置信度，通常定义为

$\alpha$与$\gamma$同样都是hyper parameter，需要交叉验证来确定，对置信度定性的解释也就是用户对指定商品的行为越多，我们就越有理由认为用户对这个商品是真正感兴趣的，比较类似于统计检验中置信度的概念。设想我们在网购时买一个自己喜欢的东西基本上都要看来看去好多次甚至好多天，但如果是帮人买，多数情况下的行为是与这个商品只接触一次，买完即走。更generalized的想法是，把$c_{ui}$解释为用户对商品的行为权重，对电商而言，如果仅仅浏览过，权重最小，浏览次数大于一定阈值时，权重次之，加购过，权重再次加大，购买过，权重最大。

如果考虑得再复杂一点，可以把$x_u^T y_i$更加具体化，比如加上用户的属性特征$U$，有过行为的商品embedding归一化特征$I$，扩充用户的隐因子矩阵$x$，就变为

对于$y_i$，如果有必要的话也可以同样进行这种扩充方式处理，从而解决一些数据不足或冷启动的问题。

学习算法

最小化目标函数的方法主要有梯度下降法和交替最小二乘法（Alternative Least Square, ALS），接下来分别简要说明一下。

梯度下降

其实严格的来说，矩阵分解的梯度下降应该叫做随机梯度下降（逐个元素更新）。先看最基础的，定义损失函数

，待更新参数为$x_{ik}$和$y_{kj}$，每一步梯度更新后两个参数分别为

加上正则项后，形式类似，

这里有一点需要注意，并不是$X$和$Y$中的所有元素都需要按顺序依次更新，因为目标矩阵的稀疏性导致大量rating值缺失，所以只需要更新那些$e_{ij}$不为空对应的user和item矩阵元素。

python的简单实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

import numpy
def matrix_factorization(R, X, Y, rank, iter, lr = 0.01, gamma =0.02):
    Y = Y.T
    # update user-item latent factor
    for step in xrange(iter):
        for i in xrange(R.shape[0]):
            for j in xrange(R.shape[1]):
                if R[i][j] > 0:
                    eij = R[i][j] - numpy.dot(X[i,:],Y[:,j])
                    for k in xrange(rank):
                        X[i][k] = X[i][k] + 2 * lr * (eij * Y[k][j] - gamma * X[i][k])
                        Y[k][j] = Y[k][j] + 2 * lr * (eij * X[i][k] - gamma * Y[k][j])
    return X, Y.T
R = numpy.array([[5,3,0,1],
     [4,0,0,1],
     [1,1,0,5],
     [1,0,0,4],
     [0,1,5,4]])
rank = 2 
X = numpy.random.rand(R.shape[0], rank)
Y = numpy.random.rand(R.shape[1], rank)
X_new, Y_new = matrix_factorization(R, X, Y, rank, 1000)
R_new = numpy.dot(X_new, Y_new.T)
print "predict matrix:\n", R_new	
print "raw matrix:\n", R
R = R.reshape(-1)
R_new = R_new.reshape(-1)
mse = 0
for i in xrange(R.size):
    if R[i] > 0:
        mse += pow(R[i] - R_new[i], 2) 
print "MSE: ", mse/R.size

输出结果

1
2
3
4
5
6
7
8
9
10
11
12
13

predict matrix:
[[ 4.95397969  2.96469808  4.39008599  1.00365562]
 [ 3.96264341  2.38721232  3.71827269  1.00055567]
 [ 1.00646214  0.98090633  5.85147223  4.94890212]
 [ 0.99598939  0.8966756   4.82086649  3.96964276]
 [ 1.2039566   1.01871901  4.97353667  3.98151943]]
raw matrix:
[[5 3 0 1]
 [4 0 0 1]
 [1 1 0 5]
 [1 0 0 4]
 [0 1 5 4]]
MSE:  0.000506024533095

ALS

从目标函数$e_{ij}^2$的形式上可以看出来，这是个non-convex function，但却是bi-convex的。也就是说，在已知$x$的情况下，就是个关于$y$的quadratic形式的function，同理在已知$y$的情况下，就是个关于$x$的quadratic形式的function，而quadratic形式是一定能找到全局最优的。针对这种问题，我们就可以固定其中一个变量来更新另一个变量，然后做一次相反的操作，迭代多次，就可以获得最下二乘下的优化解，所以这种方法就称之为交替最小二乘。正是由于在每一次迭代都可以获得真正意义的全局最优，而非梯度下降方法每次迭代只在梯度方向移动一小步，因此ALS在理论上要比gradient descent方法收敛快很多。

开始推导，这里我们只针对带正则项的explicit feedback的目标函数形式，

先固定$y_i$，求$x_u$，求导有

令上式等于0，直接求最优，可得$x_u$表达式

简单解释下各个符号含义。假设用户维度为$N$维，商品维度为$M$维，隐因子的rank为$K$维，用户$u$打过分的商品为$m$个，那么$Y_{I_i}$代表用户$u$打过分的item集合的向量堆叠，即$K \times m$维，$R(u, I_i)$用户$u$打过分的商品得分，为一个$m*1$列向量，$I$为单位向量，维度为$K \times K$，$x_u$即为用户$u$的向量表示，是一个$k \times 1$的列向量。在更新完$x_u$后，同理可以更新$y_i$，由于目标函数是对称的，就不推导了，直接上公式

含义和上面的刚好相反。如果商品$i$被$n$个用户打过分，那么$X_{I_u}$代表商品i被打过分的user集合的向量堆叠，即$K \times n$维，$R(i, I_u)$为商品$i$被打过的得分，为一个$n \times 1$的列向量，$I$为单位向量，维度为$K*K$，$y_i$即为商品$i$的向量表示，是一个$k \times 1$的列向量。在实际应用里，由于矩阵的求逆操作计算量很大，通常就通过解线性方程组的方法来求$x_u$和$y_i$。

python的简单实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

import numpy as np
def matrix_factorization(R, rank, iter, gamma =0.02):
	#initialization
	X = np.random.rand(R.shape[0], rank)
	Y = np.random.rand(R.shape[1], rank)
	I = np.eye(rank)
	for step in xrange(iter):
		for user, rating in enumerate(R):
			is_rating_index = np.nonzero(rating)
			A = np.dot(Y[is_rating_index].T, Y[is_rating_index]) + gamma * I
			B = np.dot(Y[is_rating_index].T, rating[is_rating_index])
			# using solve method instead of calculating inverse matrix
			X[user,:] = np.linalg.solve(A, B)
		for item, rating in enumerate(R.T):
			is_rating_index = np.nonzero(rating)
			A = np.dot(X[is_rating_index].T, X[is_rating_index]) + gamma * I
			B = np.dot(X[is_rating_index].T, rating[is_rating_index])
			Y[item,:] = np.linalg.solve(A, B)
	return X, Y
R = np.array([[5,3,0,1],
     [4,0,0,1],
     [1,1,0,5],
     [1,0,0,4],
     [0,1,5,4]])
rank = 2 
X, Y = matrix_factorization(R, rank, 10)
R_new = X.dot(Y.T)
print "predict matrix:\n", 	R_new
print "raw matrix:\n", R
R = R.reshape(-1)
R_new = R_new.reshape(-1)
mse = 0
for i in xrange(R.size):
    if R[i] > 0:
        mse += pow(R[i] - R_new[i], 2) 
print "MSE: ", mse/R.size

输出结果

1
2
3
4
5
6
7
8
9
10
11
12
13

predict matrix:
[[ 5.0161259   2.9859823  -3.84990048  1.01292524]
 [ 3.9720155   2.38887852 -2.78909332  0.9972788 ]
 [ 0.96012708  1.16133008  5.5264977   4.90613676]
 [ 1.04836492  1.09127496  4.15699704  3.94456546]
 [ 0.50838622  0.809576    4.99343708  4.15301915]]
raw matrix:
[[5 3 0 1]
 [4 0 0 1]
 [1 1 0 5]
 [1 0 0 4]
 [0 1 5 4]]
MSE:  0.00514865377649

至此，矩阵分解的基本原理和求解方法都已经啰嗦完了，但是现实应用中其实远没有这么简单，比如关于隐反馈的定义（用户-商品打分的量化），大数据量的内存问题（spark ALS处理亿量级的用户）等。总的来说坑还是很多的，所以这篇文章也只能算是从入门到高级入门。

参考资料

Matrix factorization techniques for recommender systems
Large-scale parallel collaborative filtering for the netflix prize
Collaborative filtering for implicit feedback datasets

看到一篇关于deep learning一些小trick的博客，感觉对于初学者可能帮助很大，但老司机应该对这些所谓的“黑魔法”烂熟于心。不管怎么说，还是囊括了大部分目前主流的一些tricks，就我本人而言也都在工作中用了这些小技巧，只不过平时都当做common sense了并没有太在意，因此也想着整理记录下来。

• 在每一个epoch结束后，一定要对数据做shuffle。也就是说要确保每轮迭代时mini-batch中的数据是不一致的

• 基于DL对大数据量的高可用性，尽可能的扩充数据。最常见的应该是图片分类问题，比如对图片进行旋转、镜像、加噪、白化等等（就像keras的image augmentation）。像在公司里比如提用户训练样本时候就可以通过滑动时间窗口的方法来获取更多数据

• 在训练大规模数据和模型前，先对数据进行一波小比例采样，如果采样数据能够使模型效果足够好的话，说明你的模型最终是可以收敛的——这个trick感觉真的没有太多人会做，如果做的话一般也都是在程序debug时候为了减少训练时间，大多数情况下都是拿到一批数据直接真刀真枪的干

• 永远都要使用dropout以防止过拟合，尤其是要在神经元比较多的全连接或卷积层后——现在一般都要随手加个dropout吧，要不总感觉少点什么

• 避免使用LRN pooling，尽量使用max pooling，因为快！

• 和sigmoid说bye-bye，和tanh说bye-bye，原因很简单：容易饱和，gradient vanishing，ReLU和PreLU明显是目前最好的选择

• 在max pooling层之后用ReLU或者PreLU，而不是之前，道理也很简单：max pooling之后维度减小，可以减少不少的计算量

• 尽量别用ReLU，过时啦！投入PreLU的怀抱！因为ReLU在初始阶段容易把训练卡死，PreLU的alpha选个0.1，完爆ReLU——这个结论感觉下的过于鲁莽，虽然理论上是这样的，但是实验里也没见过PreLU比ReLU好到哪里，但是对于训练初始阶段的情况还真没关注过，以后可以对比实验下

• 使用Batch Normalization。不多说，和dropout都差不多，加一下已经成习惯了。最近又看了BN的原作者新搞出了一个Batch Renormalization，消除了没个mini-batch中数据的差异性，据说更牛逼

• 对数据做预处理时映射到-1~1区间，而不是减去他们的均值——估计都是经验之谈，可能每份数据所呈现的结果都不太一样，个人习惯是做z-score，映射到0~1

• 尽量使用轻量级的模型，因为当你把一个庞大的model放到server上时效率的影响可能对用户体验并不是很好，即使这个工作会使你的模型准确率不够高

• 如果使用轻量级的模型，尽量做ensemble，如果ensemble了5个network，基本大约可以使准确度提搞3%——这玩意居然给量化出来了，感觉也得看是什么network吧

• 尽可能用xavier initialization做参数初始化，但是只用在全连接层，别用在CNN层上——应该就是告诉你初始化的时候weights的方差取个啥值

• 在CNN中可能的地方使用1*1卷积核，会增加spatial locality，可以自己控制升维或者降维，同时也可以把模型做的很deep——谷歌爸爸用了也说好

• 没有好的GPU，就别搞DL了

• DL不是神，理解好你要解决的问题，别就会傻套现成的网络结构

以上。

参考：The Black Magic of Deep Learning - Tips and Tricks for the practitioner

前言

从研究生时候搞Kaggle比赛到现在工作，一直接触xgboost，可以说是无论是用来直接用来做训练还是利用模型生成表达能力更强的特征然后与其他模型融合，目前来看在工业界应该是最流行和普遍使用的机器学习算法之一。文档、调参技巧和一些技术细节也看了很多次，索性把脑子里的东西整理出来作为学习笔记记录下来。

Xgboost(Extreme Gradient Boosting)实际上是Gradient Boosting Decision Tree(GBDT)的一个变种或者称为升级，成名于Kaggle的一次比赛，后来作者Tianqi Chen不断迭代优化，最终形成了目前比较成熟的版本。

模型

目标函数

首先，一个基于树的模型，基础肯定是Decision Tree。那么对于一个监督学习问题，无论是分类还是回归，如果有多棵不同tree的参与，一个样本最终所被预测的得分可以看成是这些tree每个预测结果的累加，数学上可以写为

这里$K$为tree的个数，$f_k$为每棵树在函数空间$F$中所对应的预测函数，因此这个监督学习问题的目标函数就可以由损失函数和正则项的加和定义出来了

这里如果我们回忆一下Random Forest，可以发现rf的损失函数其实也可以写成这种形式，即树的组合再加上正则约束，所以看上去gbdt和rf没什么两样嘛。但他们之间的本质区别就在于如何去优化这个$obj$。rf是并行训练每棵树作为弱分类/回归器，最后对这些树做了加权或是投票；而gbdt则是串行增量训练每棵树，最终将每棵树加到一起。换句话说，rf是Bagging的思想，gbdt是Boosting的思想。

事实上，最终需要学习的函数就是包含树结构和叶子节点得分的$f_i$。我们利用一种增量学习的方法，也就是一棵树一棵树的迭代学习，每次学习完一棵树就保存下来，然后在此基础上再新加入一棵树来不断降低目标损失。因此在第$t$个step我们学习到的$\hat y_i^{(t)}$可以写成如下形式：

如果我们的损失函数定义为MSE的话，那么目标函数就可以变为这种形式：

其中$constant$是与$y_i$和$\hat y_i^{t-1}$有关的一坨。现在我们把目标函数搞成了这种形式比较优雅的形式：一个$f$的一阶项、二阶项组合，但是实际应用的时候，可能面对的损失函数多种多样，比如hinge、logloss等等，因此就需要一个比较general的表达式，即对loss function进行二阶泰勒展开，这里我个人认为也是xgboost的重点和亮点之一：

最终的在训练到第$t$棵树时的目标函数为

一旦我们自己定义好了损失函数，一阶微分和二阶微分$g_i$、$h_i$也就被唯一确定了，也就是变相定义了目标函数。regulation项$\Omega$还需要指定一下。对于每棵树$f$，其实可以表达为下面这种形式

$w_q$为一棵树所有叶子节点（叶子数为$T$）的打分向量，$q$是每个样本所对应叶子节点的映射函数。我们将所有叶子节点向量的平方和与叶子节点数量的summation作为regulation term：

这里可能过于晦涩，举个例子。假设s_a被分到了leaf_1，打分为0.4；s_b被分到了leaf_2，打分为0.6；s_c、s_d、s_e被分到了leaf_3，打分为1.0，那么$q(s_a) = 1$，$q(s_b) = 1$，$q(s_c, s_d, s_e) = 1$，$\Omega = 3\gamma + \frac{1}{2}\lambda(0.4^2+0.6^2+1.0^2)$。虽然正则项的定义方式多种多样，但是作者提到了，这种定义方式在实际应用中效果是比较好的。

学习过程

到这里，宏观问题基本已经解决了，接下来就要考察每棵树的最优树结构，换句话说就是最优化每个父节点分叉时所利用的信息。有了之前的一些定义，又可以将目标函数重写成如下形式

其中$I_j$定义为所有属于叶子节点$j$的样本集合。如果继续定义

，这里可以理解为一棵树中落在其中一个叶子节点上所有样本的一阶导求和和二阶导求和项，那么上面的式子就可以化简为

优雅的形式再次出现，$w_j$代表第$j$个叶子节点上的得分，与上面式子中各种乱七八糟的东西都无关，quatratic形式$Ax^2 + Bx$使得$\omega$可解

很明显，$obj$越小，说明我们构建的这个树结构就越好，最好的方法就是我们遍历所有可能的树结构，which is impossible。所以针对每棵树利用这个目标函数作为节点分裂准则对每个节点进行分裂，只要分裂后的树结构比分裂前的树结构要好，那么就分裂，否则不分裂，在这一点上xgboost和decision tree通过熵增益的方法来分裂树的思想是一致的，只不过所采用的信息增益度量方法不同而已。由$obj^*$可以得到一个结点分裂后的信息增益为

其中$L$和$R$分别代表左结点和右结点。这里规则就是：如果$Gain>0$，结点分裂，否则不分裂。对于连续特征，最简单的做法就是先对所有样本进行特征排序，依次对排序后的序列样本分割后计算$G$和$H$，并找出$Gain$最大值所对应的最佳分割点；对于分类特征，可以one-hot编码后按照连续特征一样处理，最终找出最佳特征的最佳分割点即可完成依次结点分裂过程，当满足一定条件（如树最大深度为N或叶子节点样本个数最少为M）时，即可终止一棵树的学习过程，训练完成。

参数

xgboost刚出来那会Kaggle的比赛几乎都在疯狂调参，所以对于一般结构化数据的classification/regression类比赛都可以变相的理解为xgboost调参+特征工程+model ensemble大赛，熟悉了之后基本调参的维度也就5~6维，参数具体含义作者也明确的给出了（https://github.com/dmlc/xgboost/blob/master/doc/parameter.md）。调参具体可以采用Grid Search或者Random Search大法，如果数据量大、学习率低、树深度深再加上树棵数又比较多，真的是比较耗时的一件事。而且实话实话说，如果不是搞比赛的话真的没必要去在tuning上花过多时间，即使调了一手好参数，得到一手好结果，数据量一大，之后上线后泛化能力真的不好说。

不过另一方面，现在深度学习火起来之后大家对xgboost似乎也没有那么迷信了，都在用一些比较时髦的模型。但不可否认的是目前来看xgboost在工业界对于一些传统的分类问题地位感觉还是蛮高的，而且使用的方法也是五花八门，之前仿照Facebook在2014年提出的方法（Practical lessons from predicting clicks on adsat facebook），用xgboost生成的高维稀疏特征+ffm离线评测感觉也还可以接受，至少基本与xgboost的single model指标持平。

总结

最后简单一下整个xgboost的训练过程:

1. 建立第$t$棵树，从根节点分裂开始
2. 对于当前节点，计算$g_i$和$h_i$，并通过$Gain$来判断是否分裂和最佳分割点
3. 达到给定条件时，终止训练当前树结构，每个训练样本的新预测结果都是前N棵树与当前树预测结果的累加和$\hat y_i^{(t)} = \hat y_i^{(t-1)} +\eta f_t(x_i)$ ($\eta$为学习率，相当于对每棵树模型都指定一个衰减系数，减小模型variance，防止过拟合)
4. 回到1，训练第$t$+1棵树，直到等于指定最大树个数n_estimators

参考资料
Boosted Tree by Tianqi Chen
Xgboost Documentation

最近团队在搞DNN，用的都是别人搭好的框架，因此想着自己来实现一下简单的神经网络模型，更好的理解其中foward和back propagation的过程。

原理

最简单的神经网络基本上可以分为两个步骤：前向传播和后向误差传递。

前向传播

定义input layer与hidden layer之间的weights为$w_1$，hidden layer与output layer之间的weights为$w_2$。输入向量$x$与$w_1$相乘累加后通过一个非线性变换函数activation function (sigmoid, tanh, relu等)得到hidden layer中neuron的输出结果，然后hidden layer与$w_2$相乘累加后再通过activation function得到output layer中nueron的输出结果。如果中间有多个hidden layer，就不断重复这一过程（这里为了简化处理省略了bias项）。

其中$\sigma$即为activation function，如果为sigmoid函数，

其导数具有良好的性质，

而最终的output就是我们期待的输出y。

后向误差传递

后向传播的目地在于将预测结果与真实结果进行对比，并根据预测误差来对每层的weights进行更新，最简单的更新方法就是梯度下降，也就是每次迭代时在误差梯度方向移动一小步，这样在经过若干步后参数逐渐更新，误差逐渐收敛，以达到训练效果。如果我们如果将问题视为一个regression问题来处理，那么一种常见的平方误差损失函数可以表示为

求梯度，简单来讲就是求导数，在参数更新时，由于误差是在output layer才得到的，如果想对前若干层的weights求导，我们需要采取的是链式求导方法，也就是

这样误差一层一层向前传递，最终每一层的weights都会得到相对于loss的变化$\Delta$，然后再减掉$\Delta * \eta$ (学习率)，这样就完成了一次所有参数的更新

针对$w_2$而言，运用链式求导法则，则有

$w_1$由于需要再向后反向传播一层，求导显得更麻烦一点，不过依然是运用链式求导法则，

如果中间隐层增加，依然遵循这一法则向后传播误差，可以看到每向后跨越一层，就需要计算一次activation fuction的导数，这个导数最大值在0处为0.25，也就是说如果隐层为N层，最后误差向后传播到第一个隐层，误差信息最多为$\frac{\partial loss} {\partial output}*0.25^N$，已经所剩无几，这也解释了为什么sigmoid函数容易出现gradient vanishing（梯度消失现象），因此在实际应用中我们大多数是使用ReLU这种激活函数的。

值得注意的是这里也要遵循维数相容原则，简单来讲就是链式求导时的前后相乘项需要维度互相匹配，并最终相乘后维度等于输出空间的维度。

• “将他们当做一维实数然后使用链式法则，最后做维数相容的调整，使之符合矩阵乘法原则并且维数相容即可”，这种方式是一种最快速准确的策略
• “对单个元素求导，再整理成矩阵形式”这种方式是困难、过程缓慢的

完成一次向前预测和向后传递误差的过程称为一次epoch，如此反复的进行多轮迭代到一定次数或误差小于一定的阈值，即可完成模型的训练。

实现

假设现在测试数据共4个样本，每个样本有3维特征，输出为1维，因此input layer为(4, 3)，output layer为(4, 1)。设置1层4个neuron的hidden layer，其中$w_1$为(3, 4)，$w_2$为(4, 1)，代码十分简洁。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

import numpy as np
def sigmoid(x):
	return 1/(1+np.exp(-x))
def sigmoid_derivative(x):
	return x * (1 - x)
def loss(y, y_hat):
	return np.sum(np.square(y_hat - y))	
#load data
X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])
y = np.array([[0,1,1,0]]).T
# weight initialization and learning rate
w_l1 = 2*np.random.random((3,4)) - 1
w_l2 = 2*np.random.random((4,1)) - 1
lr = 0.1
for j in range(10000):
	#forward propagation
	layer_1 = sigmoid(np.dot(X,w_l1))
	layer_2 = sigmoid(np.dot(layer_1,w_l2))
	#back propagation
	delta_2 = (y - layer_2) * sigmoid_derivative(layer_2)
	delta_1 = delta_2.dot(w_l2.T) * sigmoid_derivative(layer_1)
	#update weights
	w_l2 += lr * layer_1.T.dot(delta_2)
	w_l1 += lr * X.T.dot(delta_1)
	#print loss
	if j % 2000 == 0:
		print("Iteration ", j, ": ", loss(y, layer_2))

Loss随着epoch不断增加而减小，输出结果：

1
2
3
4
5

Iteration  0 :  1.00255859758
Iteration  2000 :  0.875218177244
Iteration  4000 :  0.111818055322
Iteration  6000 :  0.028557004711
Iteration  8000 :  0.0148779596401

加了nueron上的bias项、ReLU和learning rate，更加通用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

import numpy as np
from sklearn import datasets
def sigmoid(x):
	return 1/(1+np.exp(-x))
def sigmoid_derivative(x):
	return x * (1 - x)
def relu(x):
	x[x <= 0] = 0
	return x
def relu_derivative(x):
	x[x <= 0] = 0
	x[x > 0] = 1
	return x
def mean_square(y, y_hat):
	return np.mean(np.square(y_hat - y))
def cross_entropy(y, y_hat):
	epsilon = 1e-15
	return -np.mean(y * np.log(y_hat + epsilon) + (1 - y) * np.log(1 - y_hat + epsilon))
def train(X, y, activation = "sigmoid", hidden_units = 128):
	# weight initialization
	w_l1 = 2*np.random.random((X.shape[1],hidden_units)) - 1
	w_l2 = 2*np.random.random((hidden_units,y.shape[1])) - 1
	# bias initilization
	b_l1 = np.zeros((1, hidden_units))
	b_l2 = np.zeros((1, y.shape[1]))
    # learning rate
	lr = 0.1
	for j in range(10000):
		if activation == "relu":
			layer_1 = relu(np.dot(X,w_l1) + b_l1)
			layer_2 = sigmoid(np.dot(layer_1,w_l2) + b_l2)
			delta_2 = (y - layer_2) * sigmoid_derivative(layer_2)
			delta_1 = delta_2.dot(w_l2.T) * relu_derivative(layer_1)
		
		else:
			layer_1 = sigmoid(np.dot(X,w_l1) + b_l1)
			layer_2 = sigmoid(np.dot(layer_1,w_l2) + b_l2)
			delta_2 = (y - layer_2) * sigmoid_derivative(layer_2)
			delta_1 = delta_2.dot(w_l2.T) * sigmoid_derivative(layer_1)
		#update weights and biases
		w_l2 += lr * layer_1.T.dot(delta_2)
		w_l1 += lr * X.T.dot(delta_1)
		b_l2 += lr * np.sum(delta_2, axis = 0, keepdims = True)
		b_l1 += lr * np.sum(delta_1, axis = 0, keepdims = True)
		#print loss
		if j % 2000 == 0:
			print("Iteration ", j, ": ", cross_entropy(y, layer_2))
			#print(layer_2)
if __name__ == "__main__":
	data = datasets.make_classification()
	X = data[0]
	y = data[1].reshape(-1, 1)
	train(X, y,'relu')

相应的Kaggle比赛在这里

简介

　　美国的宠物收容所每年会接纳七百余万只宠物，在这当中有一些是被主人所遗弃的，有一部分是走失后被他人捡到的。这其中一些比较幸运的少数宠物会最终重回一个温暖的家，不过由于要控制收容所宠物数量，每年大概有近三百万的汪星人和喵星人会被安乐死。

数据

　　数据来源于Austin Animal Center，包含喵星人和汪星人的名字、品种、年龄等信息，目的是为了预测具有不同特征的宠物最终去向（被收养、安乐死等），并且期望能够帮助收养机构了解到具有哪些特征的宠物需要一些额外的关注。

统计结果

　　我们先对数据进行一些简单直观的可视化(Trainset + Testset)

宠物类型及品种

　　喵星人和汪星人数量相当，Mixed品种的占大多数。

性别信息

　　公母数量相当，但绝大部分是neutered（公：被阉割的，母：被摘除卵巢的）。

颜色及年龄信息

　　排名前三位的颜色分别为黑白、黑色和棕色斑点，而宠物年龄大多都不满一岁。

姓名

　　还有一个比较有趣，关于名字的信息，排名前三位分别为Bella, Max和Charlie。

阿猫阿狗的区别

　　喵星人和汪星人的区别主要体现三个方面：年龄、neutered situation和Mixed状况——喵星人的年龄更小，汪星人neutered的更多，几乎所有喵星人都是mixed。

宠物去向（Trainset Only）

　　汪星人最终返回主人身边和被收养的比例出奇的高，而喵星人最多的去向是被转移到别的地方，难道狗真的比猫要更受人欢迎么；而Sex不同的宠物最终归宿差别极小。

　　从比例上来看，mixed与unmixed宠物的outcome区别也并不大；而neutered的宠物更容易被收养，而intact的宠物更多的被transfer，另外安乐死的比例也略高。

　　宠物的年龄越大，就约容易返回主人身边；而排名前三花色的宠物最终outcome无显著差异。

　　在品种数量排名前三位汪星人中，相比较吉娃娃和拉布拉多犬，收容所中比特犬虽然数量最多，但其安乐死比例非常高，而被收养率很低。

Overview

Epiphone’s long friendship with innovator Les Paul dates back to the late 30s and early 40s when Les and fellow guitarists such as Charlie Christian and George Barnes were at the forefront of jazz guitar. Epi Stathopoulos and Les were good friends and Epi would let Les use the Epiphone factory on 14th Street in New York City at night after hours to experiment on guitar and pickup designs. This also was the era when Les, inspired by the stinging sustain heard in electric steel guitars, began dreaming of making a solidbody guitar. He built his first, the legendary “Log,” at the Epi factory in 1941. Over the years, Les continued to work closely with Epiphone luthiers, reviewing new product ideas and offering suggestions.

Now, the Epiphone Les Paul Tribute Plus honors Epiphone’s friendship with Les by combining his classic design features with legendary Epiphone quality and value with the added power of Gibson USA 57 Classic humbuckers. But this guitar is not just about recreating the “old”, it’s also about looking ahead, just as Les himself continued to do throughout his lifetime. Using 4-conductor pickup wiring, Epiphone has added two push/pull tone pots to allow for series/parallel pickup switching. The result is a Les Paul with all the standard sounds plus a huge palette of tonal possibilities at your fingertips. The Les Paul Tribute Plus also features Epiphone’s famous built-to-last hardware and electronics including a U.S. Switchcraft 3-way toggle, Mallory-150 tone capacitors, Epiphone StrapLocks, 16:1 ratio premium Grover locking tuners, and a premium hardshell case.

Body

The Epiphone Tribute Les Paul features a solid Mahogany back with a solid, carved hard Maple cap to create the ultimate combination of warmth and bite. The solid mahogany neck with a hand-fitted, glued-in joint extends well into the neck pickup cavity, creating maximum neck-to-body contact and acting almost like one continuous piece of wood. Combined with the Mahogany/Maple body, the result is a tribute to Les’ timeless guitar design with the sound that you can only get from a Les Paul. Color finishes include Black Cherry, Faded Cherry, Midnight Ebony, Midnight Sapphire, and Vintage Sunburst.

Electronics

Capturing all the power and nuances of the “Tribute’s” tonewoods is a pair of authentic Gibson USA 57 Classic humbucker pickups. With their “Patent Applied For” decal on the base plate, the 57 Classic and 57 Classic Plus are faithful replicas of the famous PAF Gibson humbuckers created by Seth Lover that helped define the “Les Paul” sound. The 57 Classic gives you a tone that is warm and subtle with full, even response that doesn’t hold back when you need that classic Gibson humbucker crunch! The 57 Classic Plus is the perfect bridge pickup and mimics humbuckers from the late 50s that often received a few extra turns of wire. This treatment gives the pickup a slightly higher output without sacrificing its rich, vintage tone. When combined, these humbuckers overdrive tube preamps to a smooth level of saturation without becoming overpowering. Both 57s Classic humbuckers feature Gibson’s special Alnico II magnets, vintage enamel coated wire, nickel plated pole pieces, nickel slugs, maple spacers and vintage-style braided wiring.

SPECIFICATIONS

This is the first test.
中文测试

1

hahaha

1.1

Mist scheme中小图片无法居中，通过修改/themes/source/css/_schemes/Mist/_posts-expanded.styl 30行可解决

1.1.1 自定义图片大小

1.1.2 为图片加caption

1.2

代码测试

1
2
3
4
5
6

// Java Test
public class HelloWorld { 
  public static void main(String args[]) {
    System.out.println("HelloWorld!"); 
  } 
}

1
2
3
4
5
6

// Scala Test
object HelloWorld {
  def main(args: Array[String]): Unit = {
    println("Hello, world!")
  }
}

1
2
3

# Python Test
def main():
  print "HelloWorld!"

2

hahaha

2.1

Quote Test:

Do not just seek happiness for yourself. Seek happiness for all. Through kindness. Through mercy.

2.2

Raw Test
content

2.3

Video Test
Video Plugin: hexo-tag-owl