Word2Vec原理简介

Word2vec，顾名思义，就是把词语料中的所有词转化为向量形式，这样自然语言就有了数学表达形式，向量化后可以聚类、近义词等运算，举一个论文中的例子，vec(“Madrid”) - vec(“Spain”) + vec(“France”)所生成的向量与vec(“Paris”)的距离是最近的。同样对于机器学习模型来说，也可以将词作为embedding的特征输入。另外，由于作者Tomas Mikolov在深度学习领域下比较出名，所以word2vec也自然而然的被归到“深度”网络了，然而了解原理后就会发现其实就是一个2-layer的浅层模型。

主要建模的方法有CBOW和Skip-gram两种，每种方法下面又可以分为Hierarchical Softmax和Negative Sampling方法。虽然看上去有点复杂，但是大致的原理很相似，下面就尽量以简单的语言和逻辑给出word2vec的原理。

CBOW

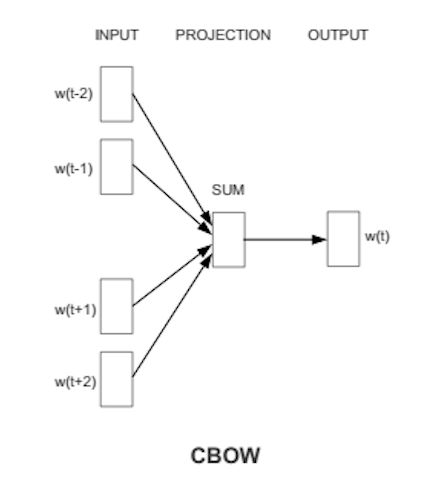
首先来看一下CBOW（Continuous Bag of Words）模型的基本结构。假设要预测词$w(t)$的向量，那么输入层是与$w(t)$相邻的几个上下文词，投影层是对这些上下文进行了向量求和运算，而输出层就是$w(t)$的概率表示。整体上来看，假设临近的词都具有一定的相似性，那么对于CBOW模型而言，目的就是要在给定词$w$上下文$Context(w)$的条件下使$w$的概率最大，这里就可以用到最大似然的思想，目标函数可以定义为对数似然函数，即

$$L= \sum log p(w|Context(w))$$

显然，对于输入层已经有了明确的表示，可以看做是监督训练中的feature，而现在的问题就是如何去构造输出层的形式，使这个两层网络能够拥有(feature, label)的形式进行迭代训练。这里就要引入另一个概念——霍夫曼编码，目的是对语料中的所有词基于出现的频率进行不等长编码。

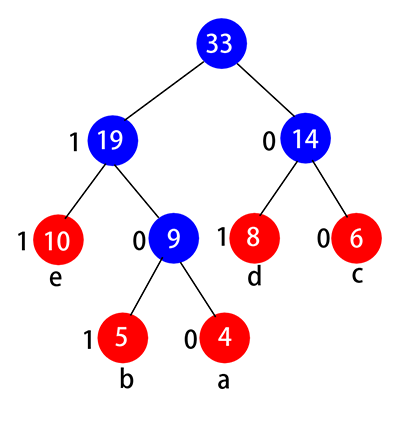
简单举个例子就可以很轻松的理解霍夫曼编码的概念。假设我们的语料为{a, b, c, d, e}，这些词在语料中出现的频率为{4, 5, 6, 8, 10}，现在我们就可以基于语料来建立一棵霍夫曼树，如下图。构建过程也很简单，即将目前集合中所有元素的两个最小值进行合并，然后用这两个最小值的求和项来代替两个最小值产生新的集合，重复这一过程直至集合中没有元素，构建过程也在下图中清晰的画了出来（这里人为规定左子节点的值大于右子节点的值）。这样看来，语料中的所有词语都会是一个单独的叶子节点（个数为size(语料)），而中间的非叶子节点就是每次的求和项（个数为size(语料)-1）。如果定义霍夫曼树中的左子节点编码为1，右子节点编码为0的话，那么每个词语都可以被唯一且不等长的编码。例如a可以被编码为100，d可以被编码为01。可以看到频率越高的词语就越出于根节点的位置，编码长度也就越短，在通信里传输数据量也就越小，这也是通信里不等长编码的奥妙所在（把本科的东西再捡起来）。

Hierarchical Softmax

OK，现在我们已经有了每个词语的霍夫曼编码，该考虑如何构建$p(w|Context(w))$了。以词语d为例，观察之前构建的霍夫曼树结构可以发现这个词语进行了两次叶子分叉：第一次从根节点分到了右子节点，第二次从当前根节点分到了左子节点。这里Hierarchical Softmax的思想就体现了出来，即把每一次非叶子节点的分裂都视为是一次二分类问题，对应的类别就是0/1，也就是节点上的编码值。如果定义1为负类，0为正类（反过来也可以），并在每次分类时采用逻辑回归模型，那么词语d的两次分类概率分别为

$$\sigma(v(d)^T \theta_1(d))\\ 1 - \sigma(v(d)^T \theta_2(d))\$$

其中$\sigma$为逻辑回归函数$\frac{1}{1+e^{-y}}，$ $v(d)$是词语d上下文的向量求和，$\theta$为每个非叶子节点所对应的辅助向量，维度与词语的向量维度一致。这样一来，把上面两个概率公式相乘后就可以以霍夫曼编码的形式得到$p(w|Context(w))$了，而每个词语的条件概率通式就可以写出来了，即

$$p(w|Context(w)) = \prod_j p(d_w^j|x_w, \theta_w^{j-1})$$

这里的$j$是每个词$w$所经过的霍夫曼树路径，$d\in {0,1}$，为在路径上的每一次分类结果。我们的目标就是取上式的似然函数$L(w,j)$最大值，未知参数只有$x_w$和$\theta_w^{j-1}$（每个词对应霍夫曼树路径上的每一个非叶子节点辅助向量），使用随机梯度上升法，不具体推导，直接给出参数的梯度：

$$\frac{\partial L(w,j)}{\partial \theta_w^{j-1}} = [1 - d_w^j - \sigma(x_w^T \theta_w^{j-1})]x_w \\ \frac{\partial L(w,j)}{\partial x_w} = [1 - d_w^j - \sigma(x_w^T \theta_w^{j-1})] \theta_w^{j-1}$$

这里的参数$\theta$可以直接利用梯度进行更新，但前面我们提到过，$x_w$实际上是$w$上下文的向量求和，而我们真正需要的是$w$的向量$v(w)$，所以在更新$v(w)$的时候需要将梯度贡献到这个词所包含的所有上下文中，并最终生成语料中每个词的词向量，学习结束。

Negative Sampling

看完Hierarchical Softmax方法后，最直观的印象可能就是霍夫曼树的构造过于麻烦，而且当语料库规模很大时，树的复杂度也随之提高，从而导致一定的训练效率问题。Negative Sampling则不采用霍夫曼树进行概率的层次计算，而是采用一种更直观、更简洁的方法。

事实上Negative Sampling可以分为两部分，一部分为Negative，另一部分为Sampling，我们先从Negative说起。如果给定词$w$及其上下文$Context(w)$，我们将此$w$视为一个正样本，其余的所有词都可以看做是负样本，除此之外再直接为每个词分配一个类似于Hierarchical Softmax方法中的辅助向量$\theta$。借助逻辑回归的思想，对于一个词$u$在$Context(w)$条件下分类后的概率为

$$p(u|context(w)) = \sigma(x_w^T \theta_u)^{L_w(u)} (1-\sigma(x_w^T \theta_u))^{1 - L_w(u)}$$

其中$L_w(u) \in {0,1}$，表示$u$是否等于$w$（需要注意的是由于我们现在讨论的还是CBOW的方法，因此这里的$x_w$和Hierarchical Softmax中的定义一样，依然是$context(w)$的向量求和）。显然，正样本只有一个，而负样本量过大，因此需要采样处理，用$Neg$表示语料中对于$w$采样后的负样本，我们的目标就是最大化

$$l(w) = \prod p(u|context(w)) = \sigma(x_w^T \theta_w) \prod_{u \in Neg}1 - \sigma(x_w^T \theta_u)$$

换句话说，就是使正样本概率尽可能高，负样本概率尽可能低。上面的式子只是针对一个词，如果是对于整个语料库$A$，依然是最大似然的思想

$$max\prod_{w \in A} l(w)$$

待更新参数依然为$x_w$和$\theta_w$，更新依然是梯度上升法，与Hierarchical Softmax基本一致，只不过后者在$\theta$的更新是基于霍夫曼树非叶子节点路径的更新，而前者则是基于$w$的正负样本做更新。

说完了Negative，还有一个重要的Sampling。从上面的基本原理中我们可以看到，负样本相对于正样本要多很多，因此需要对负样本做一定程度的采样，而采样的原则需要保证语料中词频大的词采样概率大，词频小的词采样概率小，以符合原始分布。这样看来就是一个带权采样的问题，具体解决方法可以定义每个词为其词频长度的线段，然后将所有词线段首尾相接连在一起，词频大的词自然线段就长。在采样时随机选取（0，线段总长度）的数字，采样就选择它落在范围内的词，这样就保证了采样后的词与语料中原始词的词频基本同分布。

Skip-gram

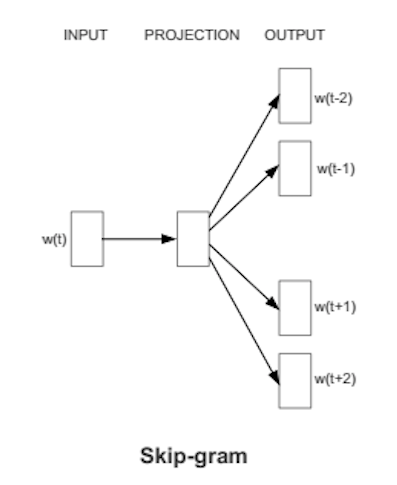
Skip-gram与CBOW的唯一区别就在于：CBOW是对$p(w|Context(w))$进行建模，而Skip-gram则是对$p(Context(w)|w)$进行建模。上面一张图可以很好的诠释二者的区别。这里的投影层只是为了和CBOW形势保持一致才加上去的，实际上不起任何作用。

针对Hierarchical Softmax方法，只需要将条件概率形式稍加改变即可

$$p(Context(w)|w) = \prod_{u \in Context(w)}\prod_j p(d_u^j|v_w, \theta_u^{j-1})$$

接下来流程完全一致，最大似然，梯度更新，迭代学习。

而对于Negative Sampling也是同样，当给定$w$时，最大化$context(w)$中所有词的似然函数，只需要将优化目标变为

$$l(u) = \prod p(z|w) = \sigma(v_w^T \theta_z) \prod_{z \in Neg(u)}1 - \sigma(v_w^T \theta_z)\\ max \prod_{w \in A} \prod_{u \in Context(w)}l(u)$$

接下来也都是老套路。

结语

关于方法的优劣和数据集、超参数以及语义评价标准有着密切的关系，因此在实际应用中也需要不断的尝试。word2vec的应用也有很多，比如将一个用户的购物历史、app浏览历史等作为一个句子，便可以学习出商品、品类或app的语义特征。google的单机多线程的code执行效率也很高。最近的一个工作是将用户的浏览的品类历史作为句子，学习出每个品类的vec，然后喂给后续的模型作为特征进行训练，只可惜特征重要性并不出众。