NMT
在Attention机制没有被发明前,最新的Neural Machine Translation(NMT)模型的结构为decoder + encoder的形式。其中encoder负责将原始文本序列的信息压缩成一个fixed-length的向量,decoder负责在给定encoder的向量及转换文本序列当前词的情况下,预测下一个词的概率。可以数学描述为如下过程:
encoder的输出:
其中$T_x$为输出文本的长度。decoder输出的条件概率:
这里的$f$都是一个关于RNN的非线性函数,例如LSTM或Bi-LSTM。
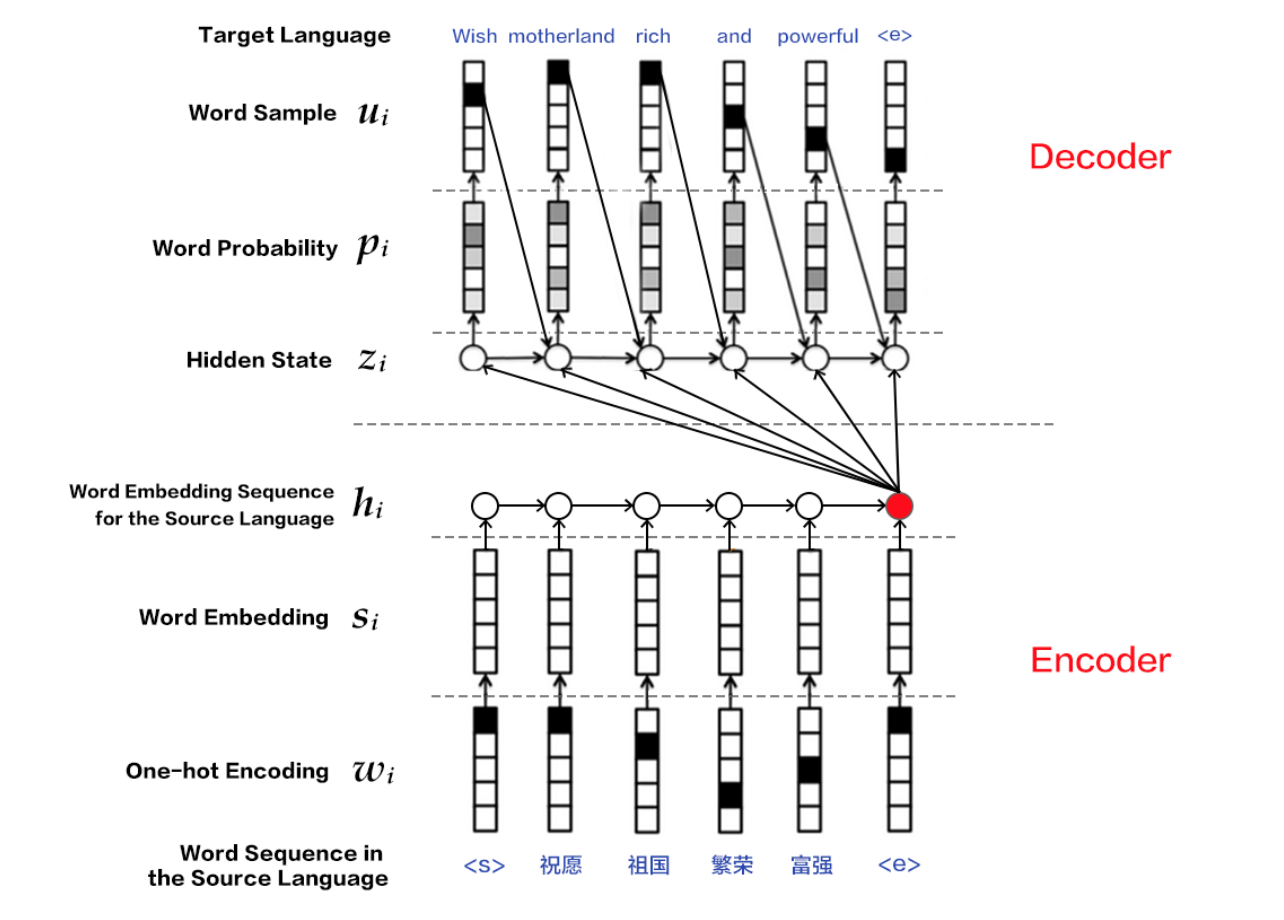
Attention
实际上,Attention机制引入的insight是由上面的建模方法的一些不足而来的。假设现在要对[I love you]做一次翻译任务,中文结果为[我爱你],那么由上面的结构encoder的输出是包含[I],[love],[you]三个词信息量的向量,当decoder来了之后,[我]、[爱]、[你]三个字的翻译都是由这一个向量作为输入,而我们人类的直觉其实应该是:当翻译[我]的时候,[I]这个词的权重权重应该更大,而其他两个词[爱]和[你]的时候,也应该对应的是[love]和[you]的大权重。因此,从这点考虑出发,encoder的输出对于每一个待翻译的词不应该都是一致的,反之应该是一种动态的,对原始文本每个词(或者理解为time step)输出的向量进行加权的形式,这种机制在人类认知里就可以解释为[注意力]机制,即对不同词翻译的时候我们注意力集中的位置也不一样,于是就有了attention的由来,上面的数学描述就发生了一些变化。由于encoder需要对于不同词产生不同的向量,encoder的输出就变为
这里$i$,$j$分别表示的是翻译文本和原始文本的词下标。这样,对于翻译文本的每个词,所产生的向量就是一种加权的形式,暂且先不理会这个权重$\alpha$是怎么来的,先看decoder的变化
其实可以看到,本质上和上面的decoder根本没发生变化,只是将$c$变成了与词下标有关的$c_i$。
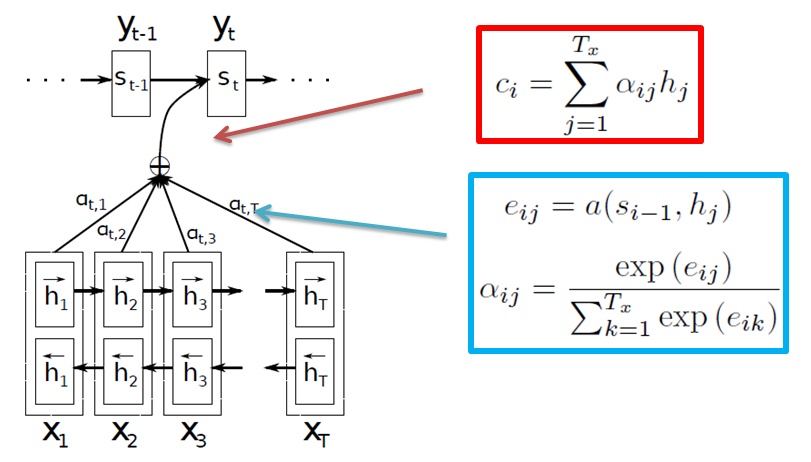
最后看$\alpha$是怎么得到的,从下标上可以发现,最终得到的$\alpha$应该是一个矩阵,大小为原始文本长度*翻译文本长度,它表示的是原始文本中第$j$个词对翻译文本中第$i$个词的权重大小(重要程度),具体计算方法为
函数$a$可以定义为一个full-conneted layer,随着整个网路一起训练,物理意义上是将翻译文本第$i-1$位的翻译词输出的向量与原始文本第$j$个原始词输出向量整合到一起做了一次操作,反映了在准确的翻译成第$i$个目标词的前提下,后者对前者的重要度。
The probability $\alpha_{ij}$, or its associated energy $e_{ij}$, reflects the importance of the annotation $h_j$ with respect to the previous hidden state $s_{i-1}$ in deciding the next state $s_i$ and generating $y_i$.
更一般的,$e$的计算方法表达为
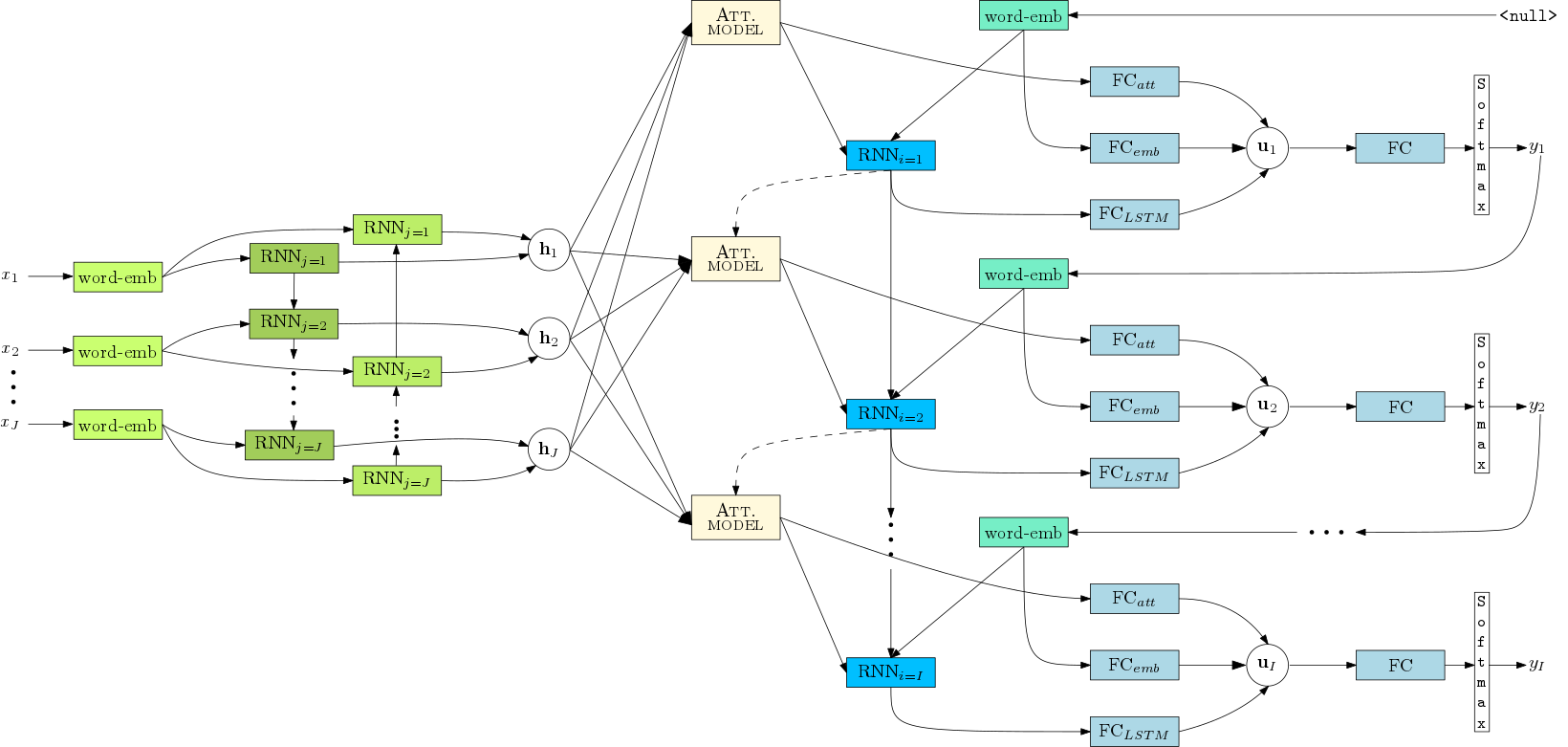
至此,基本的attention方法就结束了,下面一张图可能把整个流程描述的更清楚。值得一提的是,个人理解,attention机制的引入应该对双向RNN的依赖更强,因为翻译任务中某个待翻译词是对原始文本中特定位置的上下文敏感的,因此$h_j$中不仅要包含有上文的信息,也要包含有下文信息。
参考资料