Capsule Networks

Hinton上个月在axiv上甩出了一篇文章Dynamic Routing Between Capsules，作者在结构设计上弥补了一些cnn的设计缺陷。虽然作为行业领军人物，研究具有一定权威性，但也依然需要时间的考验和同行的不断推敲。

Capsules

在与cnn相关的研究中，这些年流行的网络框架都是基于conv+pooling的这种方式搭建的，即使是微软Resnet中引入了residual的概念，子网络依然是以这种方式组织起来。cnn中神经元的概念，无论是否共享权重，其实就是featureMap中的每一个具体的像素，是个标量。而capsules的将神经元扩展了一个维度，变成了一个向量，所以我们可以将capsules简单的理解为向量版的神经元。从网络上来说，cnn的forward过程是神经元与神经元的不断传播关系，而Capsules Network，显然，就是向量神经元之间的传播。

Model Structure

以mnist数据集为例，step by step看model的每个环节都是怎样的输出（第一个维度为batch_size）

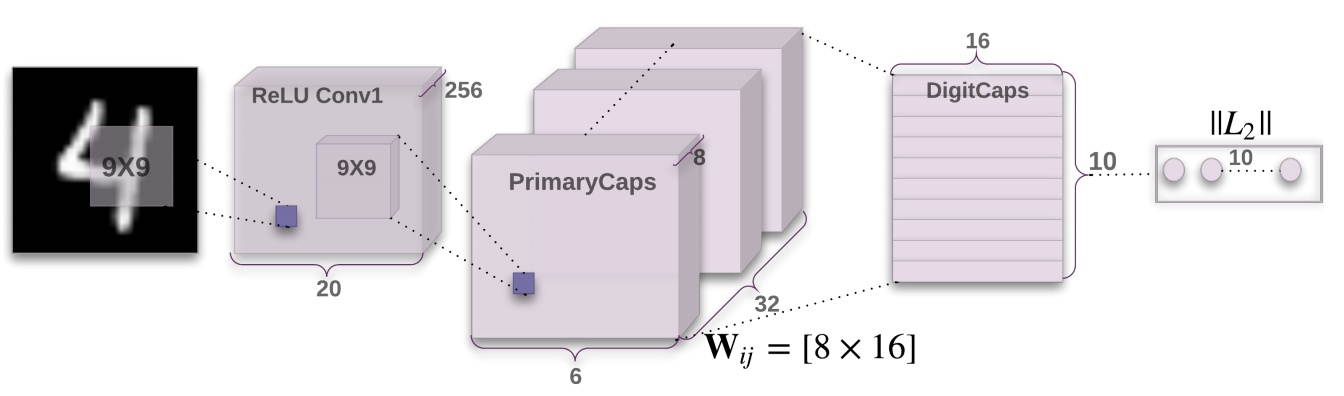
Layer One

Input: $[None,28,28,1]$

经过一层$9*9$，strides为1，通道数为256的conv layer

Output:[None,20,20,256]

Layer Two

Input:$[None,20,20,256]$

经过一层$9*9$的，strides为2，通道数为128的conv layer，按照这种方式的setting下，输出应为$[None,6,6,32]$。但如果我们将这一层的conv layer复制8份，输出就变成了$[None,6,6,8,32]$，如果我们再将这个结果reshape到$[None,6*6*32,8] = [None,1152,8]$的维度，此时capsules的概念就可以体现出来了，即，这一层共有1152个$[1*8]$的capsules向量。

Output:$[None,1152,8]$

Layer Three

Input:$[None,1152,8]$

这一层在维度上的变化略微复杂。对于一个指定index为$i$的$capsule_{i}$，其维度为$[1*8]$，引入一个维度为$[8*16]$的$Weight_{ij}$，那么

$\hat{capsule_{j|i}} = Weight_{ij}capsule_i$

上面的式子输出维度为$[1*16]$，而$i\in(1,1152)$，$j\in(1,10)$，所以共有$1152*10$个$\hat{capsule_{j|i}}$。直观上的理解是，上面的操作我们令其进行10次，一次操作代表一个类别，加上这样的capsule一共存在1152个，所以$Weight$的维度为$[1152,10,8,16]$，所以截止在$\hat{capsule}$的输出维度为$[None,1152,10,1,16]$。

接着，再引入一个维度为$[1152,10,1,1]$的bias，首先对bias做一次按第二个维度（10）的softmax压缩，维度保持不变

$c_{ij} = \frac{exp(bias_{ij})}{\sum_k exp(bias_{ik})}$

可以看到，这里的$c_{ij}$就是一个标量，用它将所有capsules建立起联系，做一次对1152个capsules的sum，即

$s_j = \sum_i c_{ij}\hat{capsule_{j|i}}$

可以看到，由于是按$i$求和，因此维度与$\hat{capsule_{j|i}}$一致（$[1*16]$），每一个$s_j$也都可以看成是capsule。由于Hinton在文中提到，capsule的模长表示概率，方向表示属性（真的很难理解。。），因此在输出层之前还要将每个capsule做一次非线性压缩

$v_j = \frac{||s_j||^2}{1+||s_j||^2} \frac{s_j}{||s_j||}$

Output:$[None,10,16]$

另外可以注意到，文章的题目中有dynamic routing的关键字，这个思想也穿插在上面的pipeline里。从公式2到公式4，可以概化为一个公式，

$cupsule_{layer2} = squashing(\sum softmax(bias)*capsule_{layer1})$

这里其实我们只进行了一次上面的操作，即将layer1的capsule transform到layer2的capsule，所以衍生出可以进行多次循环来获取更高level的capsule，而这个循环capsule高阶表达的过程就成为routing。具体的做法就是不断通过输出的高层capsule回传到低层capsule，从而更新bias（只更新bias，其余参数不更新），即

$bias_{ij} = bias_{ij} + \hat{capsule_{j|i}} v_j$

剥离上面公式的维度信息，发现$\hat{capsule_{j|i}} v_j$与$v_{ij}$均为$[16*1]$的向量，而$bias_{ij}$为一个标量，完全match，具体routing流程见下图。

在这也顺便粘上一句原文的话，说明的是每个layer之间的capsule究竟是用来干嘛的，可以好好体会一下，就一句话已经看的云里雾里了。

In convolutional capsule layers, each capsule outputs a local grid of vectors to each type of capsule in the layer above using different transformation matrices for each member of the grid as well as for each type of capsule.

Layer Four

Input:$[None,10,16]$

上面已经说到了，capsule的模长表示概率，因此直接将上层输入做一次范数即可，输出的维度即为所有类别总数

Output:$[None,10]$

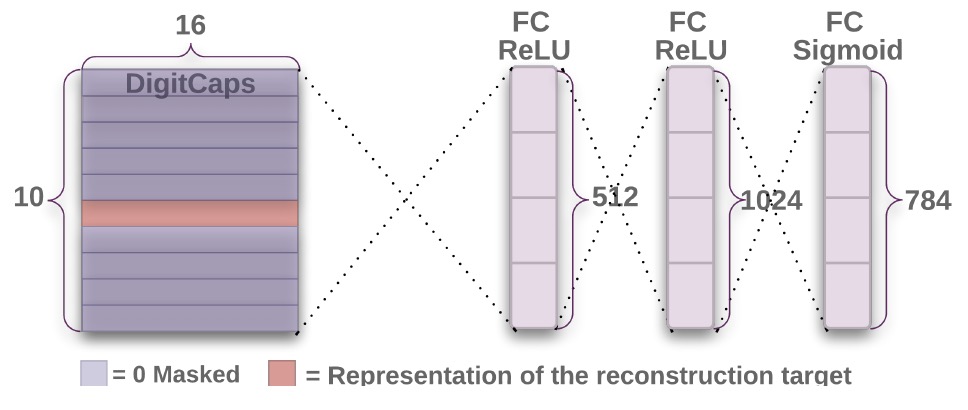
Reconstruction Layer

Input:$[None,10,16]$

上面所描述的layer均为正向预测的过程，而通过top layer的capsule还原回原始图片质量的好坏也是能证明模型表达能力的一种评价方式，所以作者又引入了reconstruction layer，来对图像进行重构。首先将Layer Four中的输入拿过来，用真实class对张量进行一次掩模，只保留真实类别对应的vector，维度为$[None,16]$，然后连续接上三个Full Connected Layer，大小分别为512，1024和728，激活函数分别为ReLU，ReLU和Sigmoid，最后再讲728维向量reshape到$[28*28]$，从而还原了原始图像。

Output:$[None,28,28,1]$

Loss Defination

说完了上面的结构，应该可以清晰的看出来，loss由两部分构成，一部分为网络正向传播上层capsule模预测为哪个class的loss-1，另一部分为重构网络还原的图片与真实图片的差异loss-2。其中loss-1使用类似于svm的margin loss，加入了一些小trick，而loss-2则使用的是重构与真实pixel-to-pixel的平方损失。形式为

$loss = loss_1 + \alpha loss_2 = T_k max(0, m^+ - ||v_k||)^2+ \lambda(1-T_k)max(0, ||v_k|| - m^-)^2 + \alpha \sum_{28}\sum_{28}(x_{ri}-x_{ti})^2$

其中$T_{k} \in (0,1)$表示图像中是否存在第k个类（这里不太一样的是，学习的图片里允许有多个类别，文章在实验中也加入两个类别分离的实验），$m^+$与$m^-$分别表示类比预测的upperBound和lowerBound，引入$\lambda(==0.5)$的作用是为了减弱不存在类capsule在初始阶段的学习，以防止对其他的capsule影响过大？（没太理解），$x_{ri}$和$x_{ti}$分别表示第$i$个重构像素与真实像素。为了尽量不影响正向构造capsule的能力，重构loss稀疏$\alpha$在文章中取得极小（0.0005）。

Implementation

Keras版本：https://github.com/XifengGuo/CapsNet-Keras

Layer的模型参数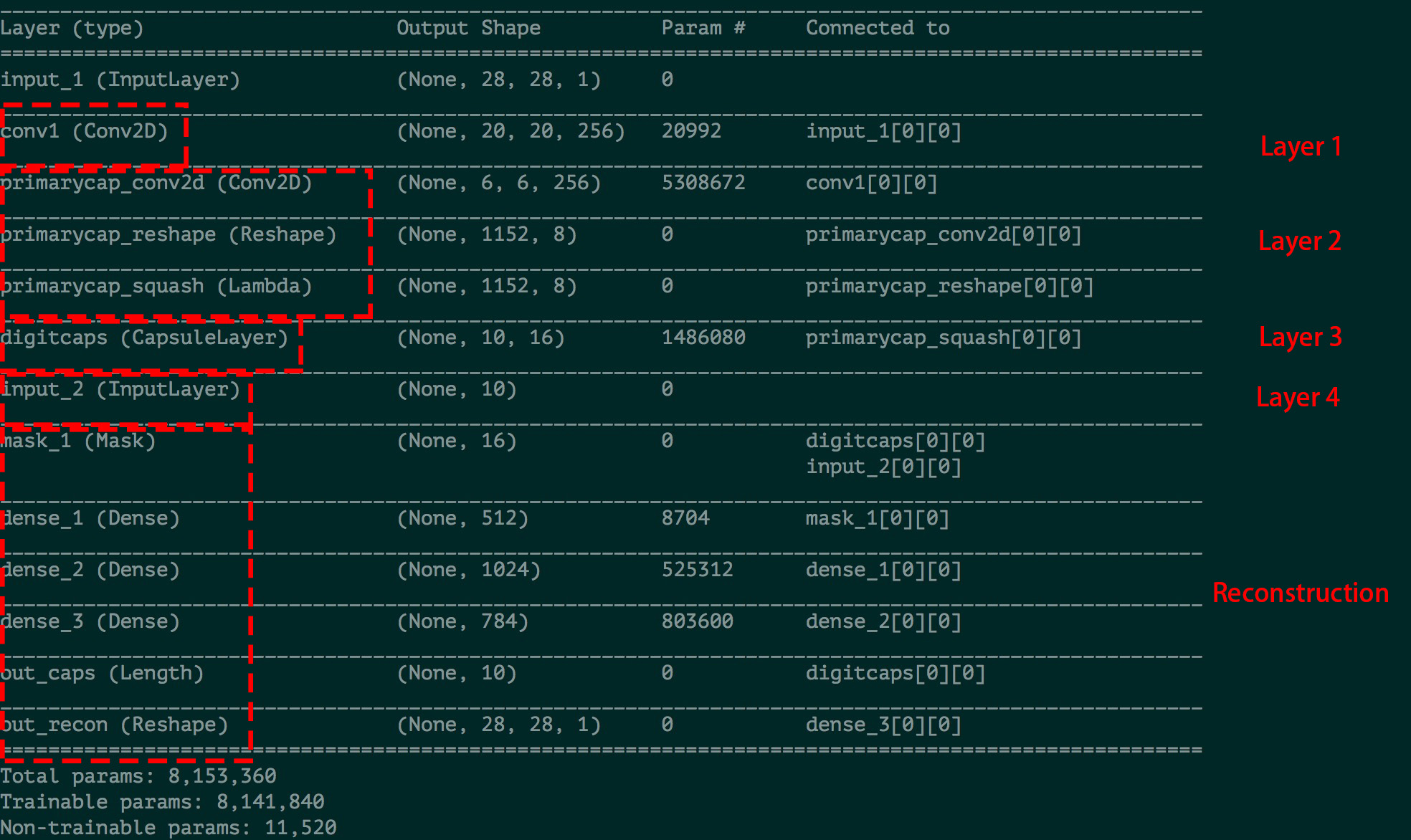

Qustions

squashing的形式为何是这样?
多次routing的作用是什么？
为什么采用margin loss？
包含有capsule的网络结构中，激活函数在哪里？
cifar数据集表现不佳的原因？