Attentional FM及源码解析

发表于 | 分类于

原理部分

书接上回，FM模型无论是对于交叉特征的捕捉能力上，还是在工业界大规模数据下的运用方面上，都具有出色的表现。因此，在深度学习火热的大背景下，各种基于FM模型和神经网络模型相结合的方法也开始频频出现。这里要说的是SIGIR 2017和IJCAI 2017的两篇文章Neural Factorization Machine和Attentional Facotrization Machine，无一例外，它们都是在FM的基础上衍生出与深度学习相关的研究。由于两篇文章的是同一团队所著，所以工作有重叠和改进部分，前一篇网络结构相对简单，因此本文主要针对Attentional Facotrization Machine展开，但也会在其中涉及Neural Factorization Machine。不仅如此，作者也同样给出了开源实现，源码解析也会在此基础上进行（Neural FM and Attention FM）。

FM模型虽然存在了所有可能的二阶特征交叉项，但本质上，并不是所有的特征都是有效的，比如一个垃圾特征a和一个牛逼特征b做交叉可能会起到一些作用，但a和垃圾特征c再做交叉基本上不会有任何作用，因此Attentional Facotrization Machine解决的问题主要就是——利用目前比较流行的attention的概念，对每个特征交叉分配不同的attention，使没用的交叉特征权重降低，有用的交叉特征权重提高，加强模型预测能力。原始的FM模型，如果忽略一阶项，可以表示为

这里我们可以把$v_i$理解为特征$x_i$的feature embedding，而上式中交叉项的表达为embedding向量的内积，因此输入的$y$直接就为标量，不需要再次的映射；但是这种内积操作如果变换为哈达玛积的操作（element-wise product）$(v_i \odot v_j) x_i x_j$，这样从Neural Network的角度去看，每个特征都交叉之后上层就变成了一个embedding layer，然后再对这个layer做一次sum pooling和映射，便可以得到输出值，即

至此，Neural Factorization Machine中所描述的已经叙述完毕，就是这么简单。而来到了Attention这篇，思想一致，只是在embedding layer的sum pooling时为每个embedding加上对应的attention，也就是权重，即

其中$\alpha$通过对embedding空间做了一次encoding并标准化得到，

另外，由于这种attention的方式对训练数据的拟合表达更充分，但也更容易过拟合，因此作者除了在loss中加入正则项之外，在attention部分加入了dropout。具体模型结构如下图：

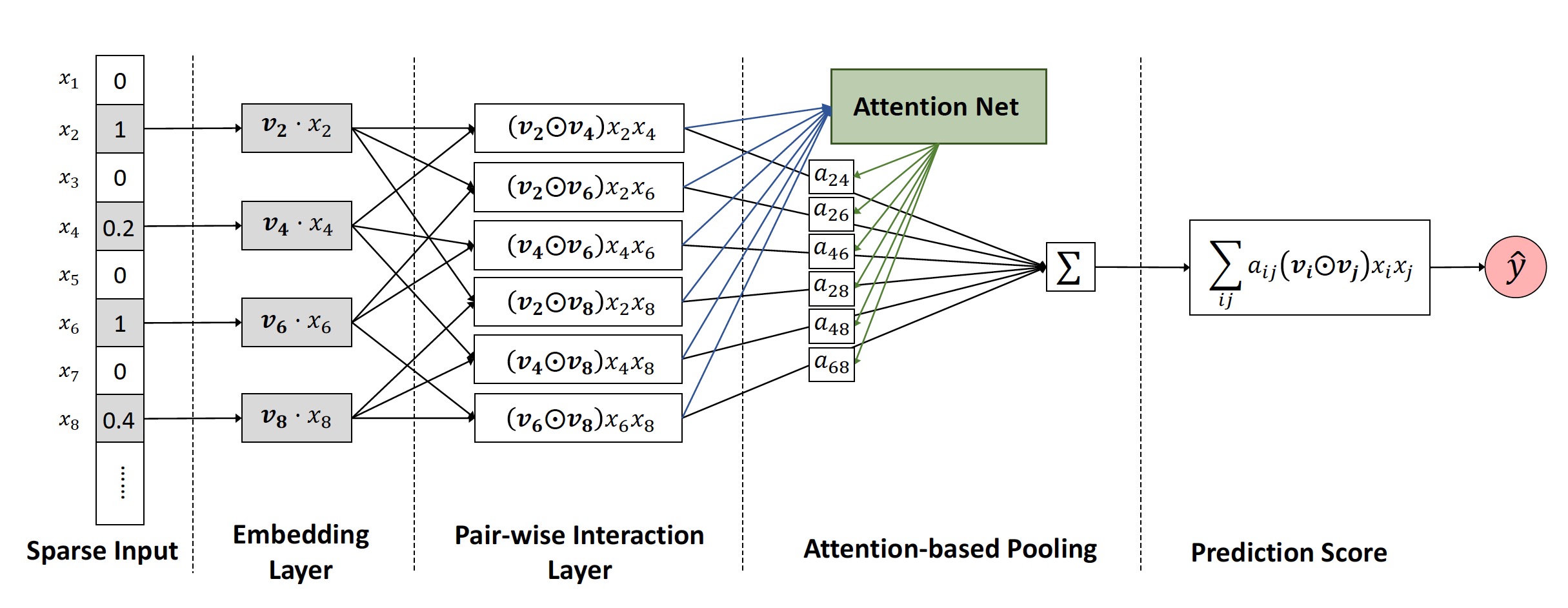
作者在Frappe和MovieLens数据集上进行了实验，AFM的表现beat掉了所有fine tuned的对比模型（LibFm、HOFM、Wide&Deep、DeepCross）。而且，使用这套框架的传统FM也要比LibFM的效果好，原因之一在于dropout的引入降低了过拟合的风险，第二在于LibFM在迭代优化时使用的是SGD方法，对每个参数的学习步长一致，很容易使后期的学习很快的止步，而Adagrad的引入使得学习率可变，因此性能更加优良。另外，attention的引入，一方面加速了收敛速度，另一方面也具有对交叉特征的可解释性（因为就是权重），类似于特征重要性。

代码部分

截取了一部分关键代码，解析在注释中体现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
def _init_graph(self):
    self.graph = tf.Graph()
    with self.graph.as_default(): 
        # Input data.
        self.train_features = tf.placeholder(tf.int32, shape=[None, None], name="train_features_afm")  # None * features_M
        self.train_labels = tf.placeholder(tf.float32, shape=[None, 1], name="train_labels_afm")  # None * 1
        self.dropout_keep = tf.placeholder(tf.float32, shape=[None], name="dropout_keep_afm")
        # Variables.
        self.weights = self._initialize_weights()
        # Model.
         # _________ Embedding part _____________
        # data为libsvm格式，且非none特征共有M‘个，且特征值均为1。data中每个feature都对应一个K维embedding
        self.nonzero_embeddings = tf.nn.embedding_lookup(self.weights['feature_embeddings'], self.train_features) # None * M' * K
        
        # 交叉项embedding layer生成，对应equation(2)
        element_wise_product_list = []
        count = 0
        for i in range(0, self.valid_dimension):
            for j in range(i+1, self.valid_dimension):
               element_wise_product_list.append(tf.multiply(self.nonzero_embeddings[:,i,:], self.nonzero_embeddings[:,j,:]))
                count += 1
        self.element_wise_product = tf.stack(element_wise_product_list) # (M'*(M'-1))/2 * None * K
        self.element_wise_product = tf.transpose(self.element_wise_product, perm=[1,0,2], name="element_wise_product") # None * (M'*(M'-1))/2 * K
        
        # _________ MLP Layer / attention part _____________
        # self.attention == True时，模型为Attention FM;
        # self.attention == False时，就退化为Neural FM
        num_interactions = self.valid_dimension*(self.valid_dimension-1)/2
        if self.attention:
            # 对应equation(4)-1
            self.attention_mul = tf.reshape(tf.matmul(tf.reshape(self.element_wise_product, shape=[-1, self.hidden_factor[1]]),self.weights['attention_W']), shape=[-1, num_interactions, self.hidden_factor[0]])
            self.attention_exp = tf.exp(tf.reduce_sum(tf.multiply(self.weights['attention_p'], tf.nn.relu(self.attention_mul + self.weights['attention_b'])), 2, keep_dims=True)) # None * (M'*(M'-1)) * 1
            self.attention_sum = tf.reduce_sum(self.attention_exp, 1, keep_dims=True) # None * 1 * 1
            # 对应equation(4)-2
            self.attention_out = tf.div(self.attention_exp, self.attention_sum, name="attention_out") # None * (M'*(M'-1)) * 1
            # 在attention部分引入dropout
            self.attention_out = tf.nn.dropout(self.attention_out, self.dropout_keep[0]) # dropout
            self.AFM = tf.reduce_sum(tf.multiply(self.attention_out, self.element_wise_product), 1, name="afm") # None * K
        else:              # Neural FM
            self.AFM = tf.reduce_sum(self.element_wise_product, 1, name="afm") # None * K
        
        # 在全连接（映射）部分二次引入dropout
        self.AFM = tf.nn.dropout(self.AFM, self.dropout_keep[1]) # dropout
        # _________ out _____________
        self.prediction = tf.matmul(self.AFM, self.weights['prediction']) # None * 1
        # 引入传统FM中的一阶项和常数项
        Bilinear = tf.reduce_sum(self.prediction, 1, keep_dims=True)  # None * 1
        self.Feature_bias = tf.reduce_sum(tf.nn.embedding_lookup(self.weights['feature_bias'], self.train_features) , 1)  # None * 1
        Bias = self.weights['bias'] * tf.ones_like(self.train_labels)  # None * 1
        self.out = tf.add_n([Bilinear, self.Feature_bias, Bias], name="out_afm")  # None * 1
        # Compute the loss.
        # 在loss中加入L2正则项
        self.loss = tf.nn.l2_loss(tf.subtract(self.train_labels, self.out)) + tf.contrib.layers.l2_regularizer(self.lamda_attention)(self.weights['attention_W'])  # regulizer
        # Optimizer.
        # 传统FM为SGD方式迭代训练，可能会导致训练不充分的情况。Ada系列的迭代方式learning rate可变，会一定程度上缓解这个现象
        if self.optimizer_type == 'AdamOptimizer':
            self.optimizer = tf.train.AdamOptimizer(learning_rate=self.learning_rate, beta1=0.9, beta2=0.999, epsilon=1e-8).minimize(self.loss)
        elif self.optimizer_type == 'AdagradOptimizer':
            self.optimizer = tf.train.AdagradOptimizer(learning_rate=self.learning_rate, initial_accumulator_value=1e-8).minimize(self.loss)
        else:
            self.optimizer = tf.train.GradientDescentOptimizer(learning_rate=self.learning_rate).minimize(self.loss)
        # init
        self.saver = tf.train.Saver()
        init = tf.global_variables_initializer()
        self.sess = self._init_session()
        self.sess.run(init)